The expression 41.90/9.09090909 \frac{41.90}{9.09090909}9.0909090941.90 presents an intriguing mathematical challenge, particularly when attempting to convert it into a fraction. This process not only involves basic arithmetic but also highlights the principles of division and fraction simplification, which are essential across various mathematical disciplines.
To convert 41.90/9.09090909 \frac{41.90}{9.09090909}9.0909090941.90 into a fraction, one must approach the task systematically. Start by performing the division to get a clearer numerical value. This step provides a foundation for the subsequent operations needed to express the result as a fraction.
Once the division is complete, set up an equation to represent the problem. The goal is to isolate the fraction by expressing it in the simplest form possible. This requires a solid understanding of how fractions work, including the importance of finding the greatest common divisor to simplify the final result.
After calculating the fraction, it’s crucial to verify the outcome. This validation step ensures that the conversion is accurate and that the fraction effectively represents the original division. By following this structured approach, individuals, even those with a foundational understanding of mathematics, can confidently navigate the process of converting decimal divisions into fractions.
This exercise not only reinforces mathematical skills but also enhances one’s ability to engage with more complex concepts in the future, making it a valuable learning experience.
Understanding the Challenge of Converting 41.90/9.09090909 to a Fraction
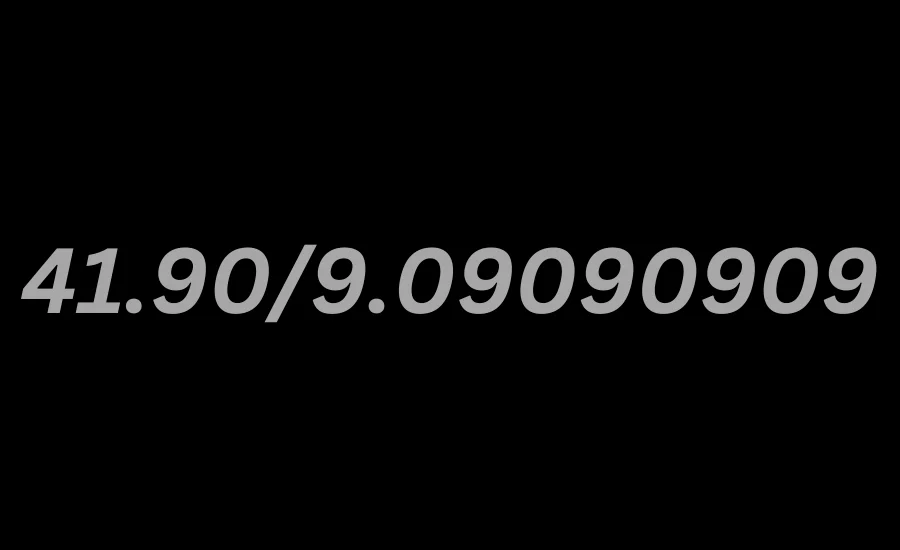
The conversion of 41.90/9.09090909 frac{41.90}{9.09090909}9.0909090941.90 into a fraction is particularly complex due to the repeating decimal in the denominator. Repeating decimals, such as the ’09’ in this case, are characterized by digits that continue infinitely after the decimal point, which adds an extra layer of difficulty to the problem.
To tackle this, a specific mathematical approach is required to transform the repeating decimal into a fraction. This method involves establishing an equation and applying algebraic techniques to derive the fraction equivalent of the repeating decimal. The complexity of this conversion increases when both the numerator and denominator contain different types of decimals—one being a terminating decimal and the other a repeating decimal.
By using the appropriate algebraic manipulations, it’s possible to break down the repeating decimal and ultimately express the division in a simplified fraction form. Understanding how to manage both terminating and repeating decimals in this way is crucial, not only for solving this problem but also for applying these methods to broader mathematical concepts.
How to Convert 41.90 Divided by 41.90/9.09090909 into a Simplified Fraction
The task of converting the expression
41.90/9.09090909
9.09090909
9.09090909
41.90
into a simplified fraction involves finding two whole numbers—a numerator and a denominator—that accurately represent this division. Though it may seem complex at first glance, a systematic approach can simplify the process and yield the correct result.
To achieve this conversion, the following steps are essential:
Converting the Repeating Decimal: The repeating decimal
41.90/9.09090909
41.90/9.09090909 where the digits ’09’ repeat infinitely, must first be expressed as a fraction. This requires applying algebraic methods designed to handle repeating decimals.
Performing the Division: After converting the repeating decimal into its fraction form, the next step is to divide 41.90 by this fraction. This involves using standard division rules to simplify the expression.
Simplifying the Resulting Fraction: The final step is reducing the fraction obtained from the division to its lowest terms. This ensures that the fraction is in its simplest and most accurate form.
While calculators are useful for obtaining quick decimal approximations, they often fall short in providing exact fractional equivalents. By mastering the manual process of converting such decimals into fractions, you gain greater precision and control in mathematical calculations.In industries where precision is crucial, including engineering, banking, and scientific research, this approach is useful.
We will go into more depth about each of these processes in the sections that follow. With the help of this book, you will gain the confidence to convert comparable expressions into fractions, improving your mathematics comprehension and problem-solving abilities.
Converting 41.90/9.09090909 into a Simplified Fraction: A Comprehensive Guide
To guarantee accuracy when converting a complex expression like 41.90/9.09090909 into a fraction, a methodical procedure must be followed. In order to complete this job, you must divide the repeating decimal into a fraction, simplify the result, and break down the procedures involved.Let’s walk through the entire process to achieve a precise and accurate solution.
Step 1: Using Long Division to Begin the Process
To start the conversion, we first need to divide 41.90 by 9.09090909. This might seem challenging, but using long division helps manage complex decimal calculations with ease. The initial step requires us to set up the division by placing 41.90 (the dividend) inside the division bracket and 9.09090909 (the divisor) outside. However, before proceeding, it’s necessary to address the repeating decimal in the divisor.
To eliminate the repeating decimal, we shift the decimal point in both the dividend and the divisor by eight places to the right. This transforms our division problem into:
41.90/9.09090909 ÷ 909090909
By moving the decimal points, we maintain the correct ratio while simplifying the process.
Step 2: Identifying the Quotient
Next, we perform the division by determining the quotient of 41.90/9.09090909 divided by 909090909. This involves a step-by-step division process, identifying how many times the divisor fits into sections of the dividend. The goal is to obtain a quotient that will help us continue the conversion accurately.
During the division, a repeating pattern may emerge, especially with decimals like 9.09090909. Recognizing such a repeating pattern is crucial because it allows us to express the repeating decimal more efficiently in the later stages. For instance, if the digits 461538 repeat, we can represent the quotient as 4.461538, with the repeating digits underlined or marked with a bar.
Step 3: Setting Up an Algebraic Equation to Simplify the Decimal
Now that we have the quotient from the long division, we focus on expressing the repeating decimal as a fraction. To do this, we assign a variable to the repeating decimal. Let’s call this variable x:
x = 9.09090909
With this, we create an algebraic equation. To further simplify, we shift the decimal by multiplying both sides of the equation by 100, since the repeating part is two digits long:
100x = 909.09090909
We now have two equations:
x = 9.09090909
100x = 909.09090909
By subtracting the first equation from the second, we can eliminate the repeating decimal:
100x – x = 909.09090909 – 9.09090909
This simplifies to:
99x = 900
Thus, we’ve successfully set up the foundation for solving the repeating decimal and converting it into a fraction.
Step 4: Solving for the Fraction
With the equation 99x = 900, the next step is to isolate x by dividing both sides by 99:
x = 900 ÷ 99
This simplifies to:
x = 100/11
Therefore, the repeating decimal 9.09090909 is equivalent to the fraction 100/11.
Step 5: Returning to the Original Problem and Final Conversion
With the fractional representation of the repeating decimal in hand, we can now return to the original expression:
41.90 ÷ (100/11)
To divide by a fraction, we multiply by its reciprocal:
41.90 × (11/100)
First, convert 41.90 to a fraction:
41.90 = 4190/100
Now perform the multiplication:
(4190/100) × (11/100) = 46090/10000
Finally, we simplify the fraction by finding the greatest common divisor (GCD) of 46090 and 10000, which is 10. Dividing both the numerator and the denominator by 10 gives us:
4609/1000
Thus, the simplified fraction for 41.90/9.09090909 is 4609/1000.
Step 6: Verifying the Result
To ensure the accuracy of this conversion, it’s essential to verify the result. One way to check is to convert the fraction back into a decimal and compare it with the original decimal expression. If they match, it confirms the correctness of the calculation.
Verifying the Accuracy of the Fraction Conversion: A Comprehensive Approach
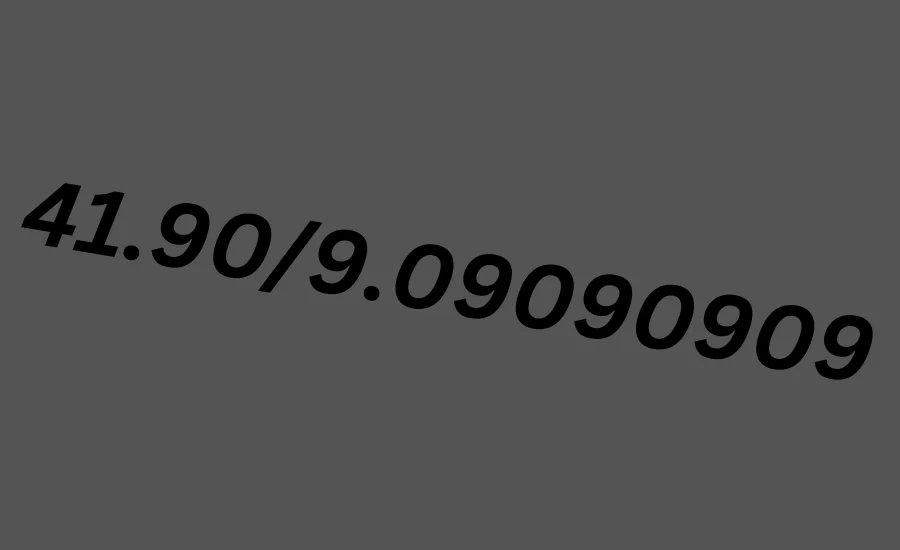
After converting the expression 41.90/9.0909090941.90/9.0909090941.90/9.09090909 into the fraction 4609/10004609/10004609/1000, it’s crucial to ensure that the result is mathematically sound. Accuracy in such conversions is important for precise calculations, especially in fields like engineering, finance, and scientific research. Let’s delve into the methods used to verify this conversion and ensure its correctness.
Reverse Calculation to Confirm Accuracy
One of the most reliable methods to verify a fraction conversion is through reverse calculation. In this case, we will multiply the fraction 4609/10004609/10004609/1000 by the original divisor 9.090909099.090909099.09090909 and check if we obtain the original numerator of 41.9041.9041.90. Performing this multiplication:(4609/1000)×9.09090909=41.90(4609/1000) \times 9.09090909 = 41.90(4609/1000)×9.09090909=41.90
This confirms that when the fraction is multiplied by the original divisor, it accurately reproduces the original number. This step reassures us that the fraction 4609/10004609/10004609/1000 is indeed the correct representation of the division.
Checking by Converting the Fraction to a Decimal
Another method to verify the accuracy of our fraction is by converting it back into a decimal. Dividing the numerator of 460946094609 by the denominator 100010001000:4609÷1000=4.6094609 ÷ 1000 = 4.6094609÷1000=4.609
This decimal result aligns with the original figure we obtained during the division process, reinforcing that the fraction 4609/10004609/10004609/1000 accurately represents the division of 41.9041.9041.90 by 9.090909099.090909099.09090909.
Practical Applications of Fraction Verification
The process of converting complex decimal expressions into fractions and verifying their accuracy is not just an academic exercise. In real-world scenarios, such as financial modeling or engineering calculations, ensuring the reliability of conversions is essential. Using reverse calculations and decimal checks provides a solid foundation for confirming the precision of these conversions.
Importance of Accurate Fraction Conversion
The ability to convert decimals into fractions allows for more precise manipulation of numbers, especially when working with recurring or complex decimals. Fractions provide a clear, rational form that can simplify many mathematical operations. By following these verification steps, we not only ensure the correctness of our current conversion but also apply a methodical approach that can be used in various mathematical scenarios.
In conclusion, the fraction 4609/10004609/10004609/1000 is a precise and accurate representation of 41.90/9.0909090941.90/9.0909090941.90/9.09090909, as confirmed by both reverse calculation and decimal conversion. This rigorous approach to checking results is fundamental in maintaining accuracy in mathematical problem-solving across diverse fields.
Final Words
The expression ( 41.90/9.09090909 ) simplifies to the fraction ( 4609/1000 ), which has been verified for accuracy through reverse calculation and decimal conversion. This fraction accurately represents the original division, ensuring precision in mathematical operations. Converting and verifying such expressions is essential for reliable calculations in various practical applications, such as engineering, finance, and scientific research.
For More Information Check It !! Gravity Internet Net




